Sistem Persamaan Linear Tiga Variabel (SPLTV) yang Bergantung dan Tidak Konsisten

Terdapat beberapa jenis selesaian dari SPLTV, yaitu selesaian yang tunggal, tak terhingga, dan tidak ada selesaian. SPLTV yang tidak memiliki selesaian akan mengarah pada hasil yang tidak konsisten, diakhiri dengan pernyataan seperti 0 = –3 atau kontradiksilainnya. Perhatikan contoh berikut.

Contoh 1: Menyelesaikan SPLTV yang Tidak Konsisten

Selesaikan SPLTV berikut dengan menggunakan cara eliminasi.

Pembahasan

1. Sistem ini tidak memiliki persamaan yang suku-x berkoefisien 1.
2. Kita masih bisa menggunakan P1 (persamaan 1) untuk memulai proses, tetapi kali ini kita akan menggunakan variabel y karena koefisiennya 1.
   Dengan menggunakan 2P1 + P2 untuk mengeliminasi y pada P2, menyisakan 7x – 2z = –4. Tetapi dengan menggunakan –2P1 + P3 untuk mengeliminasi suku-y dari P3 akan menghasilkan kontradiksi.
   
   Kita dapat menyimpulkan bahwa sistem tersebut tidak konsisten. Sehingga himpunan selesaiannya adalah himpunan kosong Ø, dan kita tidak perlu menyelesaikan sistem tersebut lebih jauh.

Tidak seperti sistem linear dua variabel, SPLTV memiliki 2 bentuk ketergantungan, yaitu bergantung linear dan bergantung kongruen. Untuk membantu dalam memahami sistem yang bergantung linear, perhatikan SPLTV yang memiliki 2 persamaan: –2x + 3y – z = 5 dan x – 3y + 2z = –1. Masing-masing persamaan tersebut merepresentasikan bidang, dan jika kedua bidang tersebut tidak sejajar, irisan dari bidang-bidang tersebut akan membentuk suatu garis. Selesaian dari sistem seperti ini dapat ditulis dengan menggunakan salah satu variabel untuk menuliskan dua variabel lainnya, atau dengan menggunakan 3 bilangan berurutan yang ditulis dengan parameter.

Suatu sistem dengan dua persamaan dan dua variabel atau tiga persamaan dan tiga variabel disebut dengan sistem persegi, yang berarti bahwa banyaknya persamaan dalam sistem sama dengan banyaknya variabel. Suatu sistem persamaan linear tidak dapat memiliki solusi yang tunggal jika banyaknya persamaan kurang dari banyaknya variabel.

Contoh 2: Menyelesaikan Sistem yang Bergantung

Selesaikan SPLTV berikut dengan menggunakan eliminasi.

Pembahasan Dengan menggunakan P1 + P2 akan mengeliminasi suku-y dari P2, menghasilkan –x + z = 4. Ini berarti bahwa (x, y, z) akan memenuhi kedua persamaan jikax = z – 4 (koordinat-x harus 4 kurangnya dari koordinat-z). Karena x dinyatakan dalam variabel z, selanjutnya substitusikan x = z – 4 ke salah satu persamaan untuk menyatakany ke dalam variabel z. Dengan menggunakan P2 kita memperoleh: (z – 4) – 3y + 2z = –1, yang menghasilkan y = z – 1 (koordinat-y harus 1 kurangnya dari koordinat-z). Jika dinyatakan dalam himpunan, maka himpunan selesaiannya adalah {(x, y, z) | x = z – 4, y =z – 1, z bilangan real}. Untuk z = –1, 0, dan 5, solusinya secara berturut akan menjadi (–5, –2, –1), (–4, –1, 0), dan (1, 4, 5). Dengan menggunakan p sebagai parameter, solusinya juga dapat ditulis menjadi (p – 4, p – 1, p) yang merupakan bentuk parametrik.

Sistem pada contoh 2 di atas merupakan sistem yang tidak persegi, sehingga secara langsung kita dapat mengetahui bahwa sistem tersebut merupakan sistem yang bergantung. Sistem pada contoh 3 berikut merupakan sistem yang persegi, tetapi hanya dengan melalui proses eliminasi kita dapat menentukan sifat dari selesaiannya.

Contoh 3: Menyelesaikan Sistem yang Bergantung

Selesaikan SPLTV berikut dengan eliminasi.

Pembahasan Sistem tersebut tidak memiliki persamaan yang koefisien variabel x-nya sama dengan 1. Kita masih bisa menggunakan P1, tetapi dengan mengeliminasi suku-z dari P2 (tidak ada suku-z di P3). Dengan P1 + P2 akan mengeliminasi suku-z dari P2 dan menghasilkan 5x – y = 4.

Selanjutnya kita akan menyelesaikan subsistem dari SPLTV yang baru tersebut. Dengan menggunakan –2P2 + P3 akan mengeliminasi suku-y di P3, tetapi juga mengeliminasi suku lainnya.

Karena P3 sama dengan 2 ∙ P2, maka sistem tersebut bergantung secara linear dan ekuivalen dengan sistem,

Dari P2 kita dapat menyelesaikan y ke dalam variabel x: y = 5x – 4. Dengan mensubstitusikan 5x – 4 ke dalam y pada P1 akan menghasilkan nilai z ke dalam variabelx.

Sehingga, himpunan selesaiannya adalah {(x, y, z) | y = 5x – 4, z = 7x – 9, x bilangan real}. Dengan menggunakan parameter p, solusinya juga dapat dituliskan menjadi (p, 5p – 4, 7p– 9) ke dalam bentuk parametrik.

Selesaian-selesaian dari sistem yang bergantung linear dapat dituliskan ke dalam x, y, atauz, tergantung dari variabel yang dieliminasi pada langkah pertama dan variabel yang kita pilih pada langkah selanjutnya.

Untuk sistem yang bergantung kongruen, persamaan-persamaan pada sistem tersebut hanya berbeda pada pengalinya. Setelah menerapkan proses eliminasi, semua variabel akan tereliminasi dan menghasilkan pernyataan yang selalu benar (seperti 3 = 3, atau yang lainnya). 

Selesaian Sistem Persamaan Linear Tiga Variabel (SPLTV)

Dalam menyelesaikan sistem persamaan linear tiga variabel (SPLTV), ingat bahwa masing-masing persamaan memiliki grafik berupa suatu bidang datar dalam ruang tiga dimensi. Bidang-bidang tersebut dapat saling berpotongan dengan bermacam-macam cara, yang menghasilkan kemungkinan himpunan selesaian yang berbeda pula. Perhatikan ilustrasi berikut.

Sistem persamaan linear tiga variabel dapat memiliki tepat satu selesaian (a, b, c), jika bidang-bidang pada sistem tersebut berpotongan tepat di satu titik (gambar a). Dengan kata lain, titik ini memenuhi semua persamaan pada sistem tersebut. Apabila bidang-bidang tersebut berpotongan pada suatu garis (gambar b), maka sistem tersebut disebut tergantung secara linear (linearly dependent) dan terdapat selesaian yang tak hingga banyaknya. Tidak seperti kasus pada dua dimensi, persamaan garis pada ruang tiga dimensi merupakan sesuatu yang kompleks, dan koordinat semua titik pada garis tersebut biasanya direpresentasikan dengan rumus pada tiga variabel berurutan, yang digunakan untuk menyatakan himpunan selesaiannya.

Jika bidang-bidang berpotongan pada semua titik, sistem tersebut disebut tergantung secara kongruen (coincidentally dependent), lihat gambar c. Hal ini mengindikasikan bahwa persamaan-persamaan pada sistem tersebut hanya berbeda pada pengali konstannya, atau dengan kata lain persamaan-persamaan tersebut sebenarnya sama. Himpunan selesaian dari kasus ini adalah sembarang tiga bilangan berurutan (a, b, c) yang memenuhi persamaan tersebut. Dan yang terakhir, suatu SPLTV mungkin juga tidak memiliki selesaian atau himpunan selesaiannya adalah himpunan kosong. Kasus ini dapat terjadi dengan cara yang berbeda-beda, dan yang paling sering muncul adalah kasus yang ditunjukkan oleh gambar d di atas. Pada kasus yang tidak memiliki selesaian ini, suatu tiga bilangan berurutan mungkin tidak memenuhi semua persamaan, hanya memenuhi satu atau dua persamaan. Untuk lebih memahami mengenai selesaian dari SPLTV, perhatikan contoh berikut.

Contoh: Menentukan Solusi SPLTV atau Bukan

Tentukan apakah tiga bilangan berurutan (1, –2, 3) merupakan selesaian dari SPLTV berikut atau bukan.

dan,

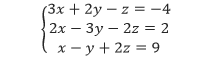
Pembahasan Substitusi 1 untuk x, –2 untuk y, dan 3 untuk z ke dalam SPLTV pertama.

Karena (1, –2, 3) tidak memenuhi salah satu persamaan pada SPLTV pertama, maka tiga bilangan berurutan tersebut bukan selesaian dari SPLTV tersebut. Selanjutnya kita gunakan substitusi yang sama pada SPLTV kedua.

Karena tiga bilangan berurutan (1, –2, 3) memenuhi ketiga persamaan pada SPLTV kedua, maka tiga bilangan berurutan tersebut merupakan solusi dari SPLTV tersebut.

Grafik Persamaan Linear Tiga Variabel (PLTV)

Posted on 26 Oktober 2013by yos3prens

Seperti kita ketahui, selesaian dari persamaan linear satu variabel (PLSV) berupa bilangan tunggal yang memenuhi persamaan tersebut. Misanya, untuk x – 5 = 1, selesaiannya adalah x = 6 dan grafiknya berupa titik tunggal pada garis bilangan, yang merupakangrafik satu dimensi. Sedangkan selesaian dari suatu persamaan linear dua variabel (PLDV), seperti 2x + y = 4, adalah pasangan-pasangan berurutan (x, y) yang memenuhi persamaan tersebut. Apabila kita menggambarkan semua selesaian dari PLDV tersebut, kita akan mendapatkan suatu garis lurus pada bidang koordinat-xy, yang merupakangrafik dua dimensi. Grafik dari selesaian PLSV dan PLDV di atas dapat ditunjukkan oleh gambar berikut.

Bagaimana dengan selesaian dari persamaan linear tiga variabel (PLTV)? Selesaian dari PLTV, seperti x + y + z = 6, berupa tiga bilangan terurut (x, y, z) yang memenuhi persamaan tersebut. Jika semua selesaian dari PLTV tersebut digambar, kita akan mendapatkan bidang dalam suatu ruang, yang disebut grafik tiga dimensi. Bidang adalah permukaaan datar yang memiliki panjang dan lebar tak terhingga, tetapi tidak memiliki ketebalan. Kita dapat menggambar grafik dari PLTV dengan menentukan titik-titik potong grafik tersebut dengan sumbu-x, sumbu-y, dan sumbu-z kemudian kita gambar suatu bidang yang melalui ketiga titik tersebut. Karena grafik x + y + z = 6 memotong sumbu-x, sumbu-y, dan sumbu-z secara berturut-turut di titik-titik (6, 0, 0), (0, 6, 0), dan (0, 0, 6), maka grafik dari persamaan tersebut dapat ditunjukkan oleh gambar (a) berikut.

Pada grafik di ruang 3 dimensi, bidang-xy sejajar dengan tanah (sumbu-y mengarah ke kanan) dan sumbu-z adalah sumbu tegak. Untuk menemukan sebarang titik yang dilalui oleh bidang x + y + z = 6, maka kita harus mencari tiga bilangan yang jumlahnya 6, seperti (2, 2, 2). Untuk menentukan posisi titik tersebut pada grafik tiga dimensi, dari titik (0, 0, 0) gerakkan 2 satuan sepanjang sumbu-x positif, kemudian lanjut 2 satuan ke arah yang sejajar dengan sumbu-y positif, dan gerakkan 2 satuan ke arah yang sejajar dengan sumbu-z positif, seperti yang ditunjukkan grafik (b) di atas. Untuk lebih memahami dalam menentukan titik-titik lainnya yang dilalui oleh bidang x + y + z = 6, perhatikan contoh berikut.

Contoh: Menentukan Solusi-solusi dari Persamaan Linear Tiga Variabel

Gunakan metode guess-and-check untuk menentukan empat titik lain yang dilalui oleh bidang x + y + z = 6.

Pembahasan Kita dapat memulainya dengan memilih x = 0, kemudian menggunakan kombinasi dua bilangan y dan z sedemikian sehingga jumlah ketiga bilangan tersebut adalah 6. Dua contohnya adalah titik-titik (0, 1, 5) dan (0, 4, 2). Kita juga dapat memilih sembarang dua bilangan x dan y, kemudian menentukan nilai z sedemikian sehingga jumlah ketiga bilangan tersebut adalah 6. Dua contohnya adalah titik-titik (5, 2, –1) dan (–3, 7, 2). 

3 komentar