Soal dan Pembahasan

Soal #1

Suatu pekerjaan dapat diselesaikan dalam waktu 50 hari oleh 30 orang pekerja. Disebabakan sesuatu hal, setelah berjalan 20 hari, pekerjaan dihentikan selama 5 hari. Agar selesai tepat waktu, diperlukan tambahan pekerja sebanyak berapa?

Pembahasan

Dengan bertambahnya pekerja, maka waktu pengerjaan akan berkurang. Maka permasalahan di atas termasuk dalam permasalahan perbandingan berbalik nilai. Untuk memahami permasalahan di atas perhatikan diagram di bawah ini:

Perhatikan pada soal, diketahui bahwa suatu perkerjaan dapat diselesakan oleh 30 orang dalam waktu 50 hari. Misalkan 1 orang selama 1 hari dapat menyelesaikan 1 pekerjaan. Maka selama 50 hari, sebanyak 30 orang dapat menyelesaikan (50 × 30 = 1.500) pekerjaan. Maka sebanyak 1.500 pekerjaan inilah yng harus diselesaikan.

1. Periode pertama. Pada periode pertama, terdapat 30 orang dan 20 hari. Sehingga banyaknya pekerjaan yang dapat diselesaikan adalah (20 × 30 = 600) pekerjaan.
2. Periode kedua. Pada periode kedua, selama 5 hari, tidak ada orang yang bekerja. Atau dengan kata lain banyaknya pekerja pada periode ini ada 0 orang. Sehingga banyaknya pekerjaan yang diselesaikan pada periode tersebut adalah (0 × 5 = 0) pekerjaan.
3. Periode ketiga. Agar pekerjaan selesai tepat waktu, ditambahkan beberapa orang pekerja. Jika awalnya banyak pekerja adalah 30 orang dan banyaknya pekerja yang ditambahkan adalah n, maka banyaknya pekerja pada periode ketiga dapat disimbolkan (30 + n) orang. Sedangkan pada periode ketiga ini terdapat waktu 50 – (20 + 5) = 25 hari untuk menyelesaikan pekerjaan tersebut. Banyaknya pekerjaan yang dapat diselesaikan pada periode ketiga dapat dicari dengan mengalikan banyaknya hari dengan banyaknya pekerja, yaitu: 25 × (30 + n) = 25 × 30 + 25 × n = 750 + 25n

Sehingga banyaknya pekerjaan yang dapat diselesaikan pada periode ketiga adalah 750 + 25n pekerjaan. Total pekerjaan yang dapat diselesaikan pada periode pertama sampai periode ketiga adalah sebanyak 600 + 0 + 750 + 25n.

Padahal sesuai rencana, selama ketiga periode tersebut, digunakan untuk menyelesaikan 1.500 pekerjaan. Sehingga,

Jadi banyaknya pekerja yang harus ditambahkan agar pekerjaan tersebut selesai tepat waktu adalah 6 orang.

Cara yang Lebih Sederhana

Penyelesaian di atas, dapat disajikan pada tabel berikut.

Dengan menggunakan perhitungan berdasarkan hasil kali, permasalahan di atas dapat diselesaikan sebagai berikut:

Jadi, tambahan pekerja yang diperlukan adalah sebanyak 6 orang.

Soal #2

Tiga buah logam yang berbentuk bola yang memiliki jari-jari 7 cm, dimasukkan ke dalam tabung yang berisi air di dalamnya. Apabila setelah logam tersebut dimasukkan, permukaan air dalam tabung tersebut naik setinggi 2 cm, tentukan jari-jari tabung tersebut!

Pembahasan

Volume tiga bola logam sama dengan volume air yang naik. Sehingga,

Jadi, jari-jari tabung tersebut adalah 7√(14) cm.

Soal #3

Perhatikan gambar berikut!

Hitunglah besar sudut a, b, c, d, e, f, g, h, p, dan n! Jelaskan bagaimana kamu dapat menemukan besar sudut d dan h!

Pembahasan

Perhatikan bahwa d = e, dan d + e + e = 180°. Sehingga diperoleh d = e = 38°. Selanjutya, dari sifat segitiga sama kaki, maka 2d + h = 180°, sehingga h = 104°. Sudut h dan kmerupakan sudut-sudut yang berpelurus, maka k = (180 – 104)° = 76°. Sedangkan sudut fdapat dicari dari persamaan 66° + e + f = 180°, sehingga diperoleh f = 76°. Karena sudut-sudut f, g, dan d saling berpelurus maka g + f + d = 180°, maka g = 66°.

Perhatikan sudut a merupakan pelurus dari sudut yang besarnya 56°, maka a = 124°. Sudut b bertolak belakang dengan sudut yang besarnya 56°, maka b = 56°. Sudut csehadap dengan sudut b, maka c = b = 56°. Selanjutnya besar n dapat dicari dengan menggunakan informasi bahwa sudut-sudut d, c, dan n berpelurus. Diperoleh n = 86°. Sedangkan besar sudut p dapat dicari dengan menggunakan jumlah sudut dalam segitiga, yaitu p + n + 56° = 180°. Diperoleh p = 38°.

Soal #4

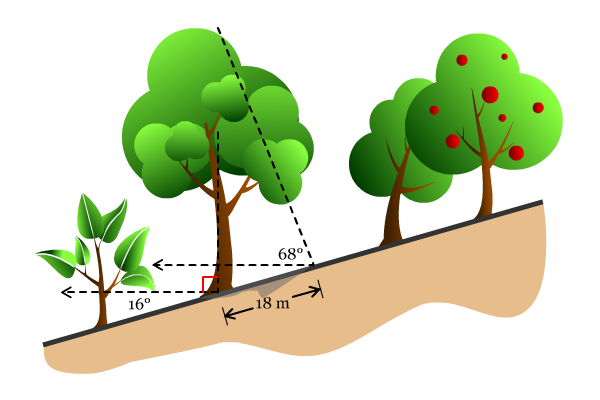
Sebuah pohon tumbuh secara vertikal pada daerah pegunungan. Permukaan tanah dari daerah pegunungan tersebut memiliki kemiringan 16° terhadap garis horizontal. Apabila panjang bayangan pohon tersebut adalah 18 meter ketika besar sudut elevasi yang dihasilkan oleh sinar matahari sebesar 68°, tentukan tinggi dari pohon tersebut?

Pembahasan

Misalkan α adalah sudut lancip yang dibentuk oleh pohon dan permukaan tanah, maka:

α + 90° + 16° = 180°

Sehingga diperoleh α = (180 – 90 – 16)° = 74°.

Misalkan β adalah sudut lancip yang dibentuk oleh sinar matahari dengan permukaan tanah, maka:

β = (68 + 16)° = 84°

Sudut-sudut α dan β merupakan sudut-sudut dalam segitiga. Selanjuntya kita tentukan besar sudut dalam segitiga yang lainnya, misalkan θ, yaitu sudut yang dibentuk oleh pohon dengan sinar matahari. Untuk menentukan besar θ, kita gunakan sifat jumlah sudut dalam segitiga.

α + β + θ = 180°

Sehingga diperoleh θ = (180 – 74 – 84)° = 22°. Setelah itu kita tentukan tinggi pohon, misalkan t, dengan menggunakan aturan sinus: (sin β) / t = (sin θ) / 18. Diperoleh, t = (18 ∙ sin β) / sin θ = (18 ∙ sin 84°) / sin 22° ≈ 47,79. Jadi, tinggi pohon tersebut adalah sekitar 47,79 meter.

Soal #5

Perhatikan gambar berikut!

Tentukan nilai x dan α!

Pembahasan

Nilai x dapat ditentukan seperti berikut:

Begitu juga untuk α, dapat ditentukan dengan menggunakan aturan cosinus seperti berikut:

Jadi, nilai x dan α secara berturut-turut adalah 47,21 cm dan 64,43°.

Soal #6

Perhatikan gambar berikut!

Tentukan nilai dari x dan y!

Pembahasan

Sesuai dengan sifat pasangan sudut-sudut alas trapesium sama kaki, x = 63°. Dengan menggunakan sifat sudut-sudut di antara sisi-sisi alas trapesium, x + y = 180°. Sehingga, y= 180° – 63° = 117°. Jadi, nilai x dan y secara berturut-turut adalah 63° dan 117°.

Soal #7

Tentukan besar dari x dan y serta keliling layang-layang LOVE!

Pembahasan

Karena sudut-sudut selain sudut puncak dari layang-layang merupakan sudut-sudut yang kongruen, maka y = 113°. Jumlah sudut dalam segiempat adalah 360°, maka x + y + 90° + 113° = 360°. Sehingga, x = 360° – (113° + 90° + 113°) = 44°.

Sesuai dengan definisi layang-layang, EV = OV = 11 cm. Demikian juga LO = LE = 19 cm. Sehingga, keliling layang-layang LOVE, K = 19 + 11 + 11 + 19 = 60.

Jadi, nilai x, y, dan keliling layang-layang LOVE secara berturut-turut adalah 44°, 113°, dan 60 cm.

Soal #8

Buatlah jaring-jaring balok berikut apabila panjang, lebar, dan tinggi dari balok tersebut secara berturut-turut memiliki perbandingan 4 : 3 : 2, dan dipotong menurut rusuk-rusuk yang berwarna merah!

Pembahasan

Untuk lebih mudah dalam mengerjakan soal ini, kita namai balok tersebut sebagai balokPQRS.TUVW.

Setelah balok tersebut diiris menurut rusuk-rusuk yang berwarna merah, yaitu rusuk-rusuk PQ, QU, TU, UV, VR, VW, dan RS, akan terbentuk jaring-jaring seperti berikut.

Untuk mengetahui perbandingan dari panjang, lebar, dan tinggi dari balok, silahkan perhatikan grid pada gambar di atas. Panjang dari balok sama dengan panjang dari rusuk-rusuk PQ, SR, TU, dan WV, yaitu 10 satuan panjang. Lebar dari balok sama dengan panjang dari rusuk-rusuk PS, QR, UV, dan TW, yaitu 7,5 satuan panjang. Sedangkan tinggi balok sama dengan panjang dari rusuk-rusuk PT, QU, RV, dan SW, yaitu 5 satuan panjang. Sehingga, p : l : t = 10 : 7,5 : 5 = 4 : 3 : 2, sesuai yang diminta soal.

Satu hal lagi, kita akan meninjau ruas garis sebagai bingkai dari daerah yang berwarna orange. Ruas garis-ruas garis tersebut memotong rusuk-rusuk PQ, TU, WV, dan SR pada balok. Pada jaring-jaring, ruas garis sebagai bingkai daerah berwarna orange tersebut juga memotong rusuk-rusuk tersebut. Sehingga, jaring-jaring yang kita lukis sesuai yang diminta oleh soal.

Soal #9

Lukislah jaring-jaring limas segi empat apabila diketahui sisi alas dan proyeksi titik puncak pada bidang alasnya seperti berikut!

Pembahasan

Jaring-jaring dari limas yang dimaksud adalah seperti berikut.

Soal #10

Perhatikan gambar berikut!

Apabila PQ = 8 cm, QR = 12 cm, RS = 10 cm, tentukan ST!

Pembahasan

Sesuai dengan sifat dua tali busur yang berpotongan di luar lingkaran, maka

QR × PR = RS × RT

Karena PR = PQ + QR = 8 + 12 = 20, dan RT = RS + ST = 10 + ST, maka

12 × 20 = 10 × (10 + ST).

Sehingga, ST = ((12 × 20) : 10) – 10 = 14.

Soal #11

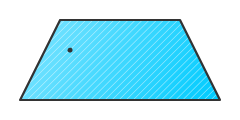
Tentukan tingkat simetri putar yang dimiliki oleh masing-masing bangun datar berikut ini.

Pembahasan

Sekarang mari kita lukis pusat titik pusat dari ketiga bangun datar tersebut.

Bangun datar pertama memiliki tingkat simetri putar 5, yaitu ketika diputar sejauh 72°, 144°, 216 °, 288°, dan 360°. Bangun datar ke-2 memiliki tingkat simetri putar 3, yaitu ketika diputar sejauh 120°, 240°, dan 360°. Sedangkan bangun datar ke-3 memiliki tingkat simetri putar 2, yaitu ketika diputar sejauh 180° dan 360°.

Soal #12

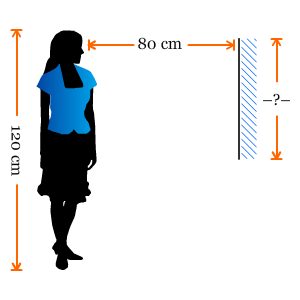
Mulan adalah seorang gadis kelas IV yang memiliki tinggi 120 cm. Ia biasanya bercermin dengan jarak 80 cm di depan cermin. Ia akan berencana pergi ke tukang cermin untuk memesan sebuah cermin. Ia akan memesan sebuah cermin dengan tinggi minimal, akan tetapi apabila dia bercermin, dia akan tetap melihat keseluruhan badannya, dari ujung kaki sampai ujung kepala. Bantulah Mulan untuk menghitung panjang cermin yang akan ia pesan tersebut! Bantulah juga di mana ia akan meletakkan cermin tersebut apabila cermin tersebut sudah jadi nantinya! (Anggap posisi mata Mulan berada 9 cm di bawah bagian teratas tubuhnya)

Pembahasan

Agar lebih mudah untuk mengerjakan soal di atas, kita ubah informasi soalnya menjadi gambar berikut.

Perhatikan bahwa segitiga segitiga ABC sebangun dengan segitiga AEF. Sehingga perbandingan sisi alas dan tingginya sama. Dengan kata lain, BC : EF = AD : AH. Sehingga,  120 : EF = 160 : 80. Diperoleh EF = (120 × 80) : 160 = 60 cm. Jadi, panjang cermin yang akan dipesan oleh Mulan haruslah 60 cm.

Sekarang perhatikan segitiga AJB dan segitiga EIB. Kedua segitiga tersebut merupakan segitiga-segitiga yang sebangun. Sehingga, perbandingan sisi-sisi yang bersesuaian sama. Dengan kata lain, AJ : EI = JB : IB. Atau 111 : EI = 160 : 80. Diperoleh EI = (111 × 80) : 160 = 55,5 cm. Jadi, apabila cermin tersebut telah jadi nantinya, ia harus memasang 5,55 cm di atas tanah.

Soal #13

Perhatikan garis bilangan berikut!

Dengan menggeser garis bilangan tersebut ke kiri atau ke kanan, tentukan hasil dari 3/4 – 1/2!

Pembahasan

Pengurangan pada pecahan pada dasarnya sama dengan pengurangan pada bilangan bulat. Pada bilangan bulat, operasi pengurangan antara dua bilangan sama dengan penjumlahan dari invers pengurangnya. Hal ini juga berlaku pada pecahan.

Sehingga,

Operasi penjumlahan di atas dapat dimodelkan oleh garis bilangan berikut.

Garis bilangan di atas diperoleh dengan menggeser garis bilangan bawah ke arah kanan, sehingga titik 0 pada garis bilangan bawah lurus dengan titik 3/4 pada garis bilangan yang atas. Dari garis bilangan di atas kita dapat melihat bahwa titik –1/2 pada garis bilangan bawah lurus dengan titik 1/4 pada garis bilangan atas. Sehingga, 3/4 – 1/2 = 1/4.

Soal #14

Bilangan-bilangan 3.154, 17.328, dan 11.027 dibagi dengan bilangan yang sama sisanya berturut-turut adalah 4, 3, dan 2. Berapa bilangan pembagi terbesar yang mungkin?

Pembahasan

Bilangan 3.154 apabila dibagi dengan suatu bilangan menghasilkan sisa 4. Sehingga, 3.154 – 4 = 3.150 akan habis dibagi oleh bilangan tersebut. Bilangan 17.328 apabila dibagi dengan bilangan yang sama akan menghasilkan sisa 3. Sehingga, 17.328 – 3 = 17.325 akan habis dibagi oleh bilangan tersebut. Bilangan 11.027 apabila dibagi dengan bilangan yang sama akan menghasilkan sisa 2. Sehingga, 11.027 – 2 = 11.025 akan habis dibagi oleh bilangan tersebut.

Selanjutnya kita akan menentukan bilangan terbesar yang dapat membagi bilangan-bilangan 3.150, 17.325, dan 11.025. Bilangan tersebut tidak lain adalah FPB dari 3.150, 17.325, dan 11.025. Kita tentukan FPB dari ketiga bilangan tersebut dengan cara sengkedan.

Sehingga kita dapat memperoleh FPB dari 3.150, 17.325, dan 11.025 adalah 32 × 52 × 7 = 1.575. Jadi, bilangan terbesar yang apabila membagi 3.154, 17.328, dan 11.025 secara berturut-turut akan menghasilkan sisa 4, 3, dan 2 adalah 1.575.

Soal #15

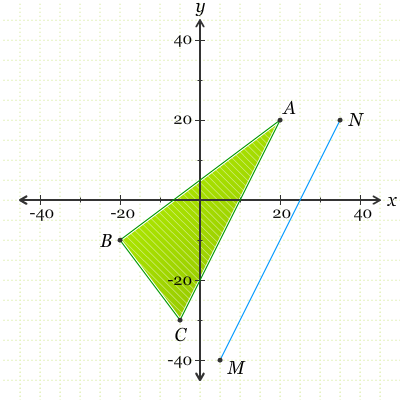
Berikut ini merupakan segitiga ABC.

Tentukanlah gradien dari ruas garis AB, BC, AC, dan MN, kemudian tentukan pasangan ruas garis yang sejajar dan tegak lurus!

Pembahasan

Sebelum menentukan gradien dari ruas garis yang diminta, kita tentukan koordinat dari masing-masing titik terlebih dahulu. Dari gambar, kita dapat peroleh A(20, 20), B(-20, -10), C(-5, -30), M(5, -40), dan N(35, 20). Sehingga, gradien dari ruas garis AB, BC, AC, dan MN dapat ditentukan seperti berikut.

Dua garis ataupun ruas garis dikatakan tegak lurus apabila hasil kali dari gradien kedua garis ataupun ruas garis tersebut sama dengan –1. Sehingga dua ruas garis yang saling tegak lurus adalah ruas garis AB dan BC, karena 3/4 × –4/3 = –1. Sedangkan dua garis ataupun ruas garis dikatakan sejajar apabila gradien dari kedua garis ataupun ruas garis tersebut sama. Sehingga, pasangan ruas garis yang sejajar adalah ruas garis AC dan ruas garis MN.

Soal #16

Tentukan hasil dari penjumlahan bilangan-bilangan berikut!

Pembahasan Untuk menyelesaikan penjumlahan bilangan-bilangan di atas, kita dapat menyederhanakan permasalahan tersebut terlebih dahulu. Perhatikan penjumlahan dari beberapa suku pertama berikut.

Dari beberapa penjumlahan di atas kita dapat mengamati bahwa hasil penjumlahannya sama dengan suatu pecahan yang pembilang dan penyebutnya berupa bilangan-bilangan yang menjadi faktor dari penyebut suku terakhir (faktor yang lebih kecil menjadi pembilang, sedangkan faktor yang lebih besar menjadi penyebut). Sehingga, kita mungkin menduga bahwa,

Atau apabila kita perumum permasalahannya: Untuk bilangan bulat n ≥ 1,

Selanjutnya, mari kita buktikan kebenaran dari dugaan kita tersebut. Untuk itu, mari kita tinjau masing-masing suku dari deret di atas.

Sehingga, kita peroleh

Apabila kita amati, penjumlahan pada ruas kanan persamaan di atas terdiri dari pasangan suku-suku yang saling invers, kecuali suku pertama, yaitu 1, dan suku terakhir, yaitu 1/(n+ 1). Sehingga, dengan menggunakan aturan kanselasi, kita mendapatkan

Sehingga, terbukti bahwa

Selanjutnya, dengan menggunakan rumus deret di atas, kita dapat menyimpulkan bahwa

Soal #17

Suatu titik D berada di dalam segitiga ABC. Buktikan bahwa AB + BC > AD + DC!

Pembahasan Mari kita gambar segitiga sebarang dengan titik D di dalamnya. Hubungkan A ke D dan D ke C. Segitiga yang terbentuk bisa berupa segitiga tumpul, akan tetapi solusi kita tidak boleh bergantung pada bentuk segitiga tersebut.

Jika kita menghubungkan titik D ke B dan perpanjang garisnya sampai memotong sisi di hadapannya di titik D0, maka jelas bahwa AB + BC > AD0 + D0C = AC karena ketaksamaan sisi-sisi segitiga. Karena berdasarkan sifat segitiga AD + DC > AC, maka juga jelas bahwaAD + DC > AD0 + D0C. Kita juga dapat menyatakan bahwa pernyataan tersebut benar untuk sembarang titik D yang terletak di antara B dan D0.

Misalkan titik D terletak pada garis tinggi yang dibentuk dari titik B ke sisi di hadapannya, seperti yang tampak pada gambar di bawah. Garis tinggi tersebut membagi segitiga ABCmenjadi dua segitiga siku-siku yang memiliki satu sisi yang sama. Berdasarkan Teorema Pythagoras, jelas bahwa semakin panjang tinggi segitiga-segitiga tersebut, maka semakin panjang sisi miringnya. Karena BD0 > DD0, maka AB > AD dan BC > DC. Sehingga, AB + BC> AD + DC.

Sayangnya, jika D tidak pada garis tinggi, maka AD tidak selalu lebih pendek daripada AB. Perhatikan gambar berikut.

Kita dapat melihat bahwa AD > AB dan DC < BC. Akan tetapi, bagaimana kita dapat memastikan bahwa AB + BC selalu lebih besar dari AD + DC?

Mungkin kita memerlukan garis bantu untuk menyelesaikan permasalahan ini. Mari kita perpanjang ruas garis AD sampai ruas garis tersebut memotong BC di E. Perhatikan gambar berikut.

Dengan menggunakan ketaksamaan segitiga yang bersesuaian kita mendapatkan:

Soal #18

Dengan mengabaikan hambatan udara, lintasan suatu bola yang dilempar pada sudut θdapat dirumuskan dengan

dimana y adalah ketinggian, x adalah jarak horizontal, g adalah percepatan gravitasi, v0merupakan kecepatan awal, dan h adalah ketinggian awal bola. Misalkan g = –10 m/s², v0= 5 m/s, dan h = 1,25 meter. Berapakah besar sudut θ yang akan menghasilkan jarak horizontal maksimum?

Pembahasan Untuk menentukan jarak tempuh bola, kita substitusi y = 0, g = –10 m/s²,v0 = 5 m/s, dan h = 1,25 ke dalam persamaan yang diberikan.

Selanjutnya, kita selesaikan x dengan menggunakan rumus kuadrat dengan a = (–sec² θ)/5, b = tan θ, dan c = 1,25.

Dari sini, kita harus menemukan nilai θ yang menghasilkan nilai maksimum x. Akan tetapi, persamaan tersebut sangatlah rumit untuk diselesaikan dengan menggunakan Uji Turunan Pertama secara manual. Sehingga kita gunakan bantuan komputer untuk menyelesaikan persamaan dx/dθ = 0. Nilai yang memaksimalkan nilai x terjadi ketika

Kesimpulan ini akan lebih jelas jika kita mensketsa lintasan bola dengan beberapa nilai θlainnya, seperti yang ditunjukkan gambar di bawah. Dari tiga lintasan yang ditunjukkan, perhatikan bahwa jarak tempuh maksimal terjadi ketika θ = 33,2°.

0 komentar