Seperti bilangan rasional yang merupakan rasio dari dua bilangan bulat, fungsi rasional adalah rasio dari dua polinomial. Secara umum,
Fungsi RasionalFungsi rasional adalah fungsi yang memiliki bentuk
Dengan p dan d merupakan polinomial dan d(x) ≠ 0. Domain dari V(x) adalah semua bilangan real, kecuali pembuat nol dari d.
Fungsi rasional yang paling sederhana adalah fungsi y = 1/x dan fungsi y = 1/x², yang keduanya memiliki pembilang konstanta dan penyebut polinomial dengan satu suku, serta kedua fungsi tersebut memiliki domain semua bilangan real kecuali x ≠ 0.
Fungsi y = 1/x
Fungsi ini disebut juga sebagai fungsi kebalikan karena setiap kita mengambil sembarang x(kecuali nol) maka akan menghasilkan kebalikannya sebagai nilai dari fungsi tersebut. Hal ini berarti x yang besar akan menghasilkan nilai fungsi yang kecil, demikian pula sebaliknya. Tabel dan grafik dari fungsi tersebut dapat dilihat seperti di bawah ini.
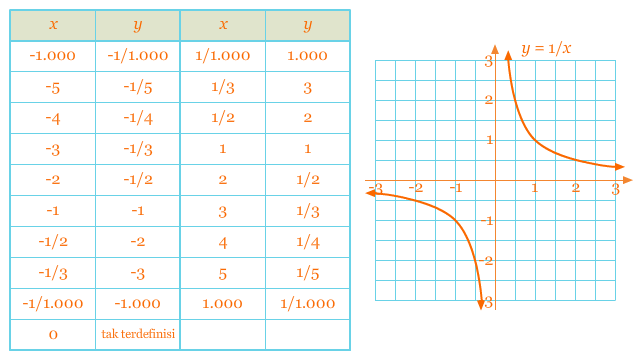
Tabel dan grafik di atas memunculkan beberapa hal yang menarik. Pertama, grafik tersebut lolos uji garis vertikal, artinya, setiap garis vertikal pada bidang koordinat Cartesius memotong grafik pada maksimal satu titik. Sehingga, y = 1/x merupakan suatu fungsi. Kedua, karena pembagian tidak terdefinisi ketika pembaginya nol, maka nol tidak memiliki pasangan, yang menghasilkan jeda pada x = 0. Hal ini sesuai dengan domain dari fungsi tersebut, yaitu semua x anggota bilangan real kecuali 0. Ketiga, fungsi tersebut merupakan fungsi ganjil, dengan salah satu cabangnya berada di kuadran I sedangkan yang lainnya berada di kuadran III. Dan yang terakhir, pada kuadran I, ketika x menuju tak hingga, nilai y menuju dan mendekati nilai nol. Secara simbolis dapat ditulis sebagaix → ∞, y → 0. Secara grafis, kurva dari grafik fungsi tersebut akan mendekati sumbu-xketika x mendekati tak hingga.
Selain itu kita juga dapat mengamati bahwa ketika x mendekati nol dari kanan maka nilai yakan mendekati bilangan real positif yang sangat besar (positif tak hingga): x → 0+, y → ∞. Sebagai catatan, tanda + atau – yang terletak di atas mengindikasikan arah dari pendekatan, yaitu dari sisi positif (+) atau dari sisi negatif (–).
Contoh 1: Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional
Untuk y = 1/x dalam kuadran III,
- Deskripsikan sifat dari ujung grafik fungsi tersebut.
- Deskripsikan apa yang terjadi ketika x mendekati nol.
Pembahasan Serupa dengan sifat grafiknya pada kuadran I, kita mendapatkan
- Ketika x mendekati negatif tak hingga, nilai y akan mendekati nol. Apabila disimbolkanx → –∞, y → 0.
- Ketika x mendekati nol dari kiri, nilai y akan mendekati negatif tak hingga. Pernyataan tersebut juga dapat dituliskan dengan x → 0–, y → –∞.
Fungsi y = 1/x²
Dari pembahasan sebelumnya, kita dapat menduga bahwa grafik dari fungsi ini akan jeda ketika x = 0. Akan tetapi karena kuadrat dari sembarang bilangan negatif adalah bilangan positif, cabang-cabang dari grafik fungsi ini akan berada di atas sumbu-x. Perhatikan bahwa fungsi y = 1/x² merupakan fungsi genap.
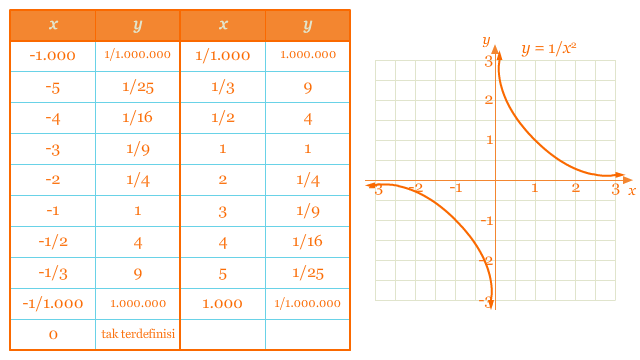
Serupa dengan y = 1/x, nilai x yang mendekati positif tak hingga, menghasilkan y yang mendekati nol: x → ∞, y → 0. Hal ini merupakan salah satu indikasi dari sifat asimtot dalam arah horizontal, dan kita mengatakan y = 0 merupakan asimtot horizontal dari fungsi y = 1/x dan y = 1/x². Secara umum,
Asimtot HorizontalDiberikan suatu konstanta k, garis y = k merupakan asimtot horizontal dari fungsi V(x) jika x bertambah tanpa batas, menyebabkan V(x) mendekati k: x → –∞, V(x) → k atau x → ∞, V(x) → k.
Pada gambar (a) di bawah ini menunjukkan garis asimtot horizontal pada y = 1, yang menggambarkan grafik f(x) sebagai translasi grafik y = 1/x ke atas sejauh 1 satuan. Gambar (b) menunjukkan garis asimtot horizontal pada y = –2, yang menggambarkan grafik g(x) sebagai pergeseran grafik y = 1/x² ke bawah sejauh 2 satuan.
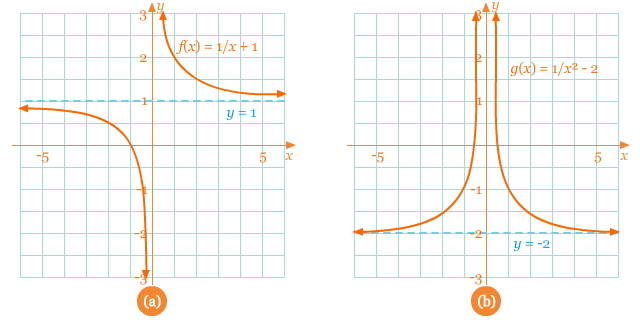
Contoh 2: Mendeskripsikan Sifat dari Ujung Grafik Fungsi Rasional
Berdasarkan gambar (b) di atas, gunakan notasi matematika untuk,
- Mendeskripsikan sifat dari ujung grafik tersebut.
- Mendeskripsikan apa yang terjadi ketika x mendekati nol.
Pembahasan
- Ketika x → –∞, g(x) → –2. Ketika x → ∞, y → –2.
- Ketika x → 0–, g(x) → ∞. Ketika x → 0+, y → ∞.
Dari contoh 2b di atas, kita dapat melihat bahwa ketika x mendekati nol, g menjadi sangat besar dan semakin bertambah tak terbatas. Hal ini merupakan indikasi dari sifat asimtot dalam arah vertikal, dan selanjutnya kita menyebut garis x = 0 merupakan asimtot vertikal untuk g (x = 0 juga merupakan asimtot vertikal untuk f). Secara umum,
Asimtot VertikalDiberikan suatu konstanta h, garis x = h merupakan asimtot vertikal untuk fungsi V jika x mendekati h, V(x) akan bertambah atau berkurang tanpa batas: ketika x → h+, V(x) → ±∞ atau ketika x → h–, V(x) → ±∞.
Mengidentifikasi dari asimtot horizontal dan vertikal sangatlah berguna karena grafik y = 1/x dan y = 1/x² dapat ditransformasi dengan menggesernya ke arah vertikal ataupun gorizontal. Fungsi,
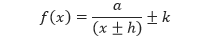
merupakan bentuk pergeseran dari fungsi y = 1/x. Sedangkan fungsi,
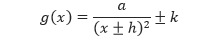
merupakan bentuk pergeseran dari fungsi y = 1/x². Selanjutnya perhatikan contoh berikut.
Contoh 3: Menuliskan Persamaan dari Fungsi Rasional
Identifikasi fungsi yang diberikan oleh grafik pada gambar di bawah, kemudian gunakan grafik tersebut untuk menuliskan persamaan fungsi tersebut. Anggap |a| = 1.
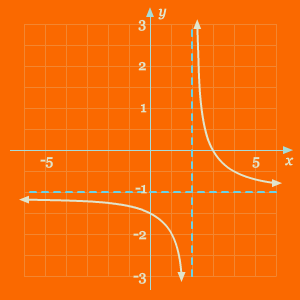
Pembahasan Dari grafik di atas, kita dapat melihat bahwa grafik tersebut merupakan pergeseran dari fungsi y = 1/x ke kanan sejauh 2 satuan dan ke bawah sejauh 1 satuan. Sehingga asimtot horizontal dan vertikal dari grafik tersebut secara berturut-turut adalahy = –1 dan x = 2. Sehingga, persamaan dari grafik di atas adalah
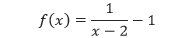
yang merupakan bentuk pergeseran dari fungsi y = 1/x. Semoga bermanfaat

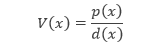
0 komentar: